故事

在现实的世界里，故事是另外一个版本：在网络的一头住着一挨踢男，另一头住着一小编。每天小编写一封垃圾邮件给挨踢男。苦命的挨踢男日日分析邮件设计过滤器来过滤小编的垃圾邮件。但聪明的小编如果一发现邮件没有成功的被寄送，那么就会在下一封里加上更多的甜言蜜语来忽悠挨踢男。较量一直进行下去，挨踢男是否能摆脱小编的骚扰呢？

以上故事都属于博弈论里的重复游戏（repeated game），它是对在线学习（online learning）最贴切的刻画：数据不断前来，我们需根据当前所能得到的来调整自己的最优策略。

熟悉机器学习的可能注意到了在线学习与离线学习的区别。前者认为数据的分布是可以任意的，甚至是为了破坏我们的策略而精心设计的，而后者则通常假定数据是服从独立同分布。这两种不同的假设带来不一样的设计理念和理论。

统计学习考虑算法所求得到的模型与真实模型的差距。数据由真实模型产生，如果能有无限数据、并在包含有真实模型的空间里求解，也许我们能算出真是模型。但实际上我们只有有限的有噪音的数据，这又限制我们只能使用相对简单的模型。所以，理想的算法是能够用不多的数据来得到一个不错的模型。

在线学习的一个主要限制是当前只能看到当前的和过去的数据，未来是未知，有可能完全颠覆现在的认知。因此，对在线学习而言，它追求的是知道所有数据时所能设计的最优策略。同这个最优策略的差异称之为后悔（regret）：后悔没能一开始就选定最优策略。我们的希望是，时间一久，数据一多，这个差异就会变得很小。因为不对数据做任何假设，最优策略是否完美我们不关心（例如回答正确所有问题）。我们追求的是，没有后悔（no-regret）。

如果与统计学习一样对数据做独立同分布假设，那么在线学习里的最优策略就是在得知所有数据的离线学习所能得到最优解。因此在线学习可以看成是一种优化方法：随着对数据的不断访问来逐步逼近这个最优解。

很早以前优化界都在追求收敛很快的优化算法，例如牛顿迭代法。而最近一些年，learning的人发现，这类算法虽然迭代几下就能迭出一个精度很高的解，但每一步都很贵，而且数据一大根本迭不动。而向来被优化界抛弃的在线学习、随机优化算法（例如stochastic gradient descent），虽然收敛不快，不过迭代代价很低，更考虑到learning算法的解的精度要求不高，所以在实际应用中这些方法通常比传统的优化算法快很多，而且可以处理非常大的数据。

当然，相对于老地主online learning，stochastic绝对是新贵。我会接下来谈这类算法，以及他们动辄数页的convergence rate的证明

下面是有公式的正文。

准确定义

我们把学生定义为Learning，老师定义为Environment。Online Learning的过程就是，learner不停的回答Environment提出的问题。 在$t$时刻，learner接收到一个领域问题$x_t$，learner提供一个答案$h_t$，同时environment会给出正确答案 $y_t$。 此时，learner就会有一个惩罚(loss) $l(h_t,y_t)$。当learner经过有无数这样的训练后，learner会学习到领域知识。 过程如下：

1. enviroment提出问题$x_t$
2. learner从策略集合$\mathcal{H}$中选着一个策略$h_t$,做出判断$h_t(x)$
3. learner根据$loss(h_t(x),y_t)$学习
4. repeat 1 如果有更多的问题

那么如何衡量一个learner过程的好坏呢？这就引入了后悔值的概念：

$$\displaystyle R(T)=\sum_{t=1}^T\ell_t(h_t)-\min_{h\in\mathcal{H}}\sum_{t=1}^T\ell_t(h).$$

h为最优策略

learner的目标就是每次挑不错的$h_t$来使得$R(T)$最小。$R(T)$是可以小于0的。毕竟最优策略是要固定h，而如果我们每次都能选择很好的$h_t$来适应问题$(x_t,y_t)$，可能总损失会更小。但这非常难。因为我们是要定好策略$h_t$，才能知道正确答案$y_t$。如果这个问题和以前的很不一样，答案也匪夷所思，那么猜对它而且一直都猜对的概率很小。而对于最优策略来说，它能事先知道所有问题和答案，所以它选择的最优策略的总损失较小的可能性更大。所以，我们一般只是关心平均$regretR(T)/T$是不是随着T变大而变小。

算法

摘录自libol

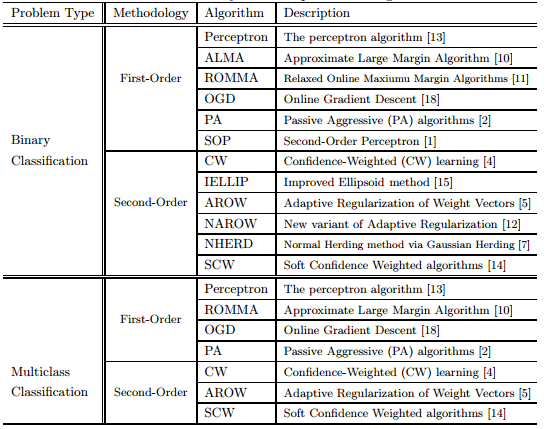
感知学习算法PLA(Perceptron Learning Algorithm)

PLA，可以简单理解成“知错就改”算法。当遇到一个错误的时候， 就修正算法。 当然PLA有很多限定条件: 假设机器要回答的问题是yes/no，目标$y \in \{-1,+1\}$,策略$h_t$是线性模型：$h_t=w_t^tx$。

PLA算法以如下两步不断循环：

1. find a misstake of $w_t$ call $(x_{n(t)},y_{n(t)})$

   $$sign(w_t^T x_{n(t)}) \neq y_{n(t)}$$

2. (try to) correct the misstake by:

   $$w_{t+1} = w_{t} + y_{n(t)} x_{n(t)}$$

当问题是线性可分的时候，PLA可以保证算法收敛到一条合适的线,详细的证明可以参考video。当问题线性不可分时，需要对算法进行适当的修改，找到一条“合适”的曲线即可。

直观上理解PLA：如果机器犯了错误，当$y$实际上是+1, 说明$w_t$ 和 $x$的夹角超过90度，偏大。需要讲$w_t$向x的方向移动一个角度。 $w_{t+1}=w_t + x$, 反之$y$实际上是-1, 说明$w_t$ 和 $x$的夹角小于90度，偏小。需要讲$w_t$向x的反方向移动一个角度。 $w_{t+1}=w_t - x$

线性分类器，是一个利用超平面来进行二分类的分类器，每次利用新的数据实例，预测，比对，更新，来调整超平面的位置。 相对于SVM，感知器不要每类数据与分类面的间隔最大化。

平均感知器(Average Perceptron)

线性分类器，其学习的过程，与Perceptron感知器的基本相同，只不过，它将所有的训练过程中的权值都保留下来，然后，求均值。

优点：克服由于学习速率过大，所引起的训练过程中出现的震荡现象。即超平面围着一个中心，忽左忽右之类.

1. For t = 1,2,…n
   1. 对$(x_t,y_t)$,如果$sign(w_t^T x_{t}) \neq y_{t}$，计算$w_{t+1} = w_{t} + y_{t} x_{t}$
2. 输出 $\sum\limits_{i = 1}^n {\frac{w_i}{n}} $

Passive Aggressive Perceptron:

修正权值时，增加了一个参数$T_t$，预测正确时，不需要调整权值，预测错误时，主动调整权值。并可以加入松弛变量的概念，形成其算法的变种。

优点：能减少错误分类的数目，而且适用于不可分的噪声情况。

1. For t = 1,2,…n
   • 对$(x_t,y_t)$,如果$sign(w_t^T x_{t}) \neq y_{t}$
   • $l_t = max \{0,1-y_t(w_t x_t) \}$
   • 计算$w_{t+1} = w_{t} + \tau_t y_{t} x_{t}$
2. 输出$w_n$

根据 $\tau_t$的不同PAP变种为：

1.$\tau_t = \frac{l_t}{\|X_t\|^2}$

2.$\tau_t = min\{C, l_t / \|X_t\|^2\}$

3.$\tau_t = \frac{l_t}{\|X_t\|^2 + 1/(2C)}$

Voted Perceptron:

存储和使用所有的错误的预测向量。

优点：实现对高维数据的分类，克服训练过程中的震荡，训练时间比SVM要好。

缺点：不能保证收敛

Confidence Weight：

线性分类器，来之google ICML2008的论文.Confidence-Weighted Linear Classification,[videolectures]相关视频介绍(http://videolectures.net/icml08_pereira_cwl/)

每个学习参数都有个信任度（概率），信任度小的参数更应该学习，所以会得到更频繁的修改机会。信任度，用参数向量的高斯分布表示。

权值w符合高斯分布N(u, 离差阵)，而 由w*x的结果，可以预测其分类的结果。

并对高斯分布（的参数）进行更新。

这种方法能提供分类的准确性，并加快学习速度。其理论依据在在于算法正确的预测概率不小于高斯分布的一个值。

AROW： adaptive regularition of weighted vector

NIPS2009的论文Adaptive Regularization of Weights code

具有的属性：大间隔训练large margin training，置信度权值confidence weight，处理不可分数据（噪声）non-separable

相对于SOP(second of Perceptron)，PA, CW, 在噪声情况下，其效果会更好.

Normal herding：

线性分类器

NHerd算法在计算全协方差阵和对角协方差阵时，比AROW更加的积极。

OGD 梯度法

Weight Majority:

每个维度都可以作为一个分类器，进行预测；然后，依据权值，综合所有结果，给出一个最终的预测。

依据最终的预测和实际测量结果，调整各个维度的权值，即更新模型。

易于实施，错误界比较小，可推导。

一点解释

no-regret是不是很难达到呢？事实证明很多简单的算法都是no-regret。举个最经典的例子，假设我们有m个专家，他们在每轮问题都会给出的答案，假设答案就两种。损失函数是0-1损失函数，答案正确损失为0，否则为1. 先考虑最简单的情况：假设至少有一个完美专家，她永远给出正确的答案。那么什么才是learner的好策略呢？最简单的很work：看多数专家怎么说罗。 learner在时刻t先挑出前t-1轮一直是给正确答案的专家们，然后采用他们中多数人给出的那个答案。

记$C_t$是前t-1轮一直是给正确答案的专家们的集合，$|C_t|$是这些专家的个数。如果learner在时刻t给出了错误的答案，那么意味着$C_t$中大部分专家都给了错误答案，所以下一时刻learner参考的专家就会少一半。因为完美专家的存在，所以$|C_t|$不可能无限变小使得小于1，所以learner不能无限犯错。事实上，$C_t$至多有$\log_2(m)$次变小机会，所以learner最多有$\log_2(m)$的损失。另一方面，最优策略当然是一直选中一位完美专家，总损失为0，所以$R(T)\le \log_2(m)$，上界是个常数.

现在考虑并没有传说中的完美专家存在的情况。这时维护$C_t$的做法就不行了，我们使用一个稍复杂些的策略。记第i个专家为$e^i$ ，对其维护一个信任度$w^i\in[0,1]$，且使得满足$\sum_{i=1}^m w^i=1$。记t时刻这m个信任度组成的向量是$w_t$，可以将其看成是关于这m专家上的一个分布，于是learner可以按这个分布来随机挑选一个专家，并用她的答案来做作为t时刻的答案。这意味着信任度高的专家被挑中的概率越高。

关键是在于如何调整$w_t$。直观上来说，对于在某一轮预测不正确的专家，我们需降低对她们的信任度，而对预测正确的，我们则可以更加的相信她们。一种常见的调整策略是基于指数的。我们先维护一个没有归一化（和不为1）的信任度u。一开始大家都为1，$u_0^i=1$. 在t时刻的一开始，我们根据i专家在上一轮的损失$\ell_{t-1}(e^i)$来做如下调整：

$$u_{t}^i=u_{t-1}^i\exp(-\eta\ell_{t-1}(e^i))$$

$\eta$是学习率，越大则每次的调整幅度越大。然后再将$u_t$归一化来得到我们要的分布：$w_t^i=u_t^i/\sum_i u_t^i$。

基于指数的调整的好处在于快速的收敛率（它是强凸的），以及分析的简单性。我们有如下结论：如果选择学习率$\eta=\sqrt{8\ln m/T}$，那么$R(T)\le \sqrt{T\ln m/2}$。

一个值得讨论的问题是，设定最优学习率$\eta$需要知道数据的总个数T，而在实际的应用中也许不能知道样本到底会有多少。所以如果设定一个实际不错的参数很trick。在以后的算法中还会遇到这类需要上帝之手设定的参数，而如何使得算法对这类控制速率的参数不敏感，是当前研究的一个热点。这是后话了。

另外一个值得注意的是，同前面存在完美专家的情况相比，平均regret的上界由$\frac{\log_2 m}{T}$增到了$\sqrt{\frac{\ln m}{2T}}$。 这两者在实际的应用中有着很大差别。例如我们的目标是要使得平均regret达到某个数值以下，假设前一种方法取1,000个样本（迭代1,000次）就能到了，那么后一种算法就可能需要1,000,000个样本和迭代。这样，在时间或样本的要求上，前者明显优于后者。类似的区别在后面还会更多的遇到，这类算法的一个主要研究热点就是如何降低regret，提高收敛速度。

在线凸优化

Primal-dual的观点

天地间都赋阴阳二气所生

算法举例

• arowpp
• oll
• sofia-ml
• libol
• jubatus
• moa

参考文献：

1. N. Cesa-Bianchi, A. Conconi, and C. Gentile. A second-order perceptron algorithm. SIAM J. Comput., 34(3):640–668, 2005
2. K. Crammer, O. Dekel, J. Keshet, S. Shalev-Shwartz, and Y. Singer. Online passiveaggressive algorithms. Journal of Machine Learning Research, 7:551–585, 2006.
3. K. Crammer, M. Dredze, and A. Kulesza. Multi-class confidence weighted algorithms. In EMNLP, pages 496–504, 2009.
4. K. Crammer, M. Dredze, and F. Pereira. Exact convex confidence-weighted learning. In NIPS, pages 345–352, 2008.
5. K. Crammer, A. Kulesza, and M. Dredze. Adaptive regularization of weight vectors. In NIPS, pages 414–422, 2009.
6. K. Crammer, A. Kulesza, and M. Dredze. Adaptive regularization of weight vectors. Machine Learning, 91(2):155–187, 2013.
7. K. Crammer and D. D. Lee. Learning via gaussian herding. In NIPS, pages 451–459, 2010.
8. K. Crammer and Y. Singer. Ultraconservative online algorithms for multiclass problems. Journal of Machine Learning Research, 3:951–991, 2003.
9. M. Fink, S. Shalev-Shwartz, Y. Singer, and S. Ullman. Online multiclass learning by interclass hypothesis sharing. In Proceedings of the 25th International Conference on Machine learning (ICML’06), pages 313–320, 2006.
10. C. Gentile. A new approximate maximal margin classification algorithm. Journal of Machine Learning Research, 2:213–242, 2001.
11. Y. Li and P. M. Long. The relaxed online maximum margin algorithm. Machine Learning, 46(1-3):361–387, 2002.
12. F. Orabona and K. Crammer. New adaptive algorithms for online classification. In NIPS, pages 1840–1848, 2010.
13. F. Rosenblatt. The perceptron: A probabilistic model for information storage and organization in the brain. Psych. Rev., 7:551–585, 1958.
14. J. Wang, P. Zhao, and S. C. H. Hoi. Exact soft confidence-weighted learning. In ICML, 2012.
15. L. Yang, R. Jin, and J. Ye. Online learning by ellipsoid method. In ICML, page 145, 2009.
16. P. Zhao, S. C. H. Hoi, and R. Jin. Double updating online learning. Journal of Machine Learning Research, 12:1587–1615, 2011.
17. P. Zhao, S. C. H. Hoi, R. Jin, and T. Yang. Online auc maximization. In ICML, pages 233–240, 2011.
18. M. Zinkevich. Online convex programming and generalized infinitesimal gradient ascent. In ICML, pages 928–936, 2003.